> FrAid
 
 
PDF -icon
PDF

FrAid Library Functions

General Mathematical Constants and Functions

E MaxVal MinVal NaN NegInf Pi
PosInf and diff greater greaterorequal integer
isInf isNaN isNextIntEven max min mul
negate nextInt nextpow2 not notequal or
quad rand round sign smaller smallerorequal
sum xor

Sampled Functions

appendS cft cloneS conv dft dft1
elemS fft fft1 firResp histogramS icft
idft idft1 ifft ifft1 inverseFilter lengthS
loadS maxS minS mulS padS randS
reverseFilter rk rk1 sampleL sampleN samples
saveS shrotS startS stepS sumS truncateS
vector

Sampled Sound (non-MIDI) Functions

loadSound playSound recordSound saveAsSound

Graphics Functions

aggregation cobweb color3D consumption iterFract julia
mandelbrot newton orbit orbit2 phase plot
plot2 plot3 plot3d plot3f plotMap spectrum
transform transform3

(undocumented) Prediction Markets Functions

pmChart predictionMarket

Complex Functions

abs acos acosh add asin asinh
atan atanh conj cos cosec cosh
cot divide equal exp imag log
multiply power real sec sin sinh
sqrt subtract tan tanh

Symbol Table Functions

assign loadSymbols

Utility Functions

False True debug debugParser exit info
isComplex isFunction isString loadScript printClassPath printDef
printDep printGen printPlugins printS printTree rename
sleep string typeOf

Graphics Helper Functions

clear closeControllers closeWindow controlVar plotOption printWindowFunction
setGridMark


E

Synopsis: 
 E;
Return Value: 
 2.718281828459045
Go to top.


MaxVal

Synopsis: 
 MaxVal;
Description: the maximum double value (1.7976931348623157E308)
Return Value: 
 1.7976931348623157E308
Go to top.


MinVal

Synopsis: 
 MinVal;
Description: the minimum double value (4.9E-324)
Return Value: 
 4.9E-324
Go to top.


NaN

Synopsis: 
 NaN;
Description: the Not a Number value - you can return NaN from your FrAid functions when an error happens;
Return Value: 
 NaN;
Go to top.


NegInf

Synopsis: 
 NegInf;
Description: the negative infinity constant;
Return Value: 
 - Infinity;
Go to top.


Pi

Synopsis: 
 Pi;
Description:
Return Value: 
 3.141592653589793
Go to top.


PosInf

Synopsis: 
 PosInf;
Description: the positive infinity constant;
Return Value: 
 Infinity;
Go to top.


and

Synopsis: 
 and( Boolean, Boolean ); | Boolean & Boolean;
Description: logical and. This is the actual implementation of the FrAid '&' operator;
Return Value: 
 Boolean
Examples: 
(2 <= 3) & (5 > 1); //(1.0 + 0.0i), same as and(2 <= 3, 5 > 1);
Go to top.


diff

Synopsis: 
diff(functionToDifferentiate,dimension_to_diff, arg1, ..., argn );
Description:derivative of a function, the dimensions start from 0 to n-1
Return Value: 
Complex
Examples: 
f(x)=diff(sin,0,x);
plot(sin,f);

diff(sin,0,Pi);
Go to top.


greater

Synopsis: 
 greater( Complex, Complex ); | Complex > Complex;
Description: checks if the first argument is greater than the second one,if the imaginary part of any of the numbers is not zero takes its absolute value.
This is the actual implementataion of the FrAid '>' operator.
Return Value: 
 Boolean
Go to top.


greaterorequal

Synopsis: 
 greaterorequal( Complex, Complex ); | Complex > =Complex;
Description: checks if the first argument is greater or equal to the second one,if the imaginary part of any of the numbers is not zero takes its absolute value.
This is the actual implementataion of the FrAid '>=' operator.
Return Value: 
 Boolean
Go to top.


integer

Synopsis: 
 integer( Complex );
Description: Returns the integer part of it's argument
Return Value: 
Complex
Examples: 
integer(2.2); // --> 2
integer(1.99); // --> 1
Go to top.


isInf

Synopsis: 
 isInf( Complex );
Description: checks for infinity, returns 1 if any of the real or imaginary parts of the argument are the double infinity
Return Value: 
 Boolean
Examples: 
isInf(PosInf); //(1.0 + 0.0i)
Go to top.


isNaN

Synopsis: 
 isNaN( Complex );
Description: checks if its argument is NaN
Return Value: 
 Boolean
Go to top.


isNextIntEven

Synopsis: 
 isNextIntEven( Complex );
Description: Returns 1 if the next integer number greater than the argument is even, 0 otherwise.
Return Value: 
 Boolean
Examples: 
 isNextIntEven( .5 ); // Returns 0
Go to top.


max

Synopsis: 
 max( Complex [, Complex, Complex, ...] );
Description: the maximum of a list of numbers
Return Value: 
 Complex;
Go to top.


min

Synopsis: 
 min( Complex [, Complex, Complex, ...] );
Description: the minimum of a list of numbers
Return Value: 
 Complex;
Go to top.


mul

Synopsis: 
 mul( Complex [, Complex, Complex, ...] );
Description: multiplies a list of numbers
Return Value: 
 Complex;
Go to top.


negate

Synopsis: 
 negate( Complex ); | -Complex;
Description: unary minus, this is the actual implementataion of the unary FrAid '-' operator;
Return Value: 
 (-1)*Complex
Go to top.


nextInt

Synopsis: 
 nextInt( Complex );
Description: Returns the next integer number greater than the argument.
Return Value: 
 Boolean
Examples: 
 nextInt( .5 ); // Returns 1
Go to top.


nextpow2

Synopsis: 
 nextpow2( Complex );
Description: Returns n - the next power of 2 so 2^n is greater than the argument passed.
Return Value: 
Complex
Examples: 
nextpow2( 8 ); // --> 3
nextpow2(8.1); // --> 4
Go to top.


not

Synopsis: 
 negate(Boolean ); | !Boolean;
Description: logical negation of the argument, this is the actual implementataion of the FrAid '!' operator;
Return Value: 
 Boolaean
Go to top.


notequal

Synopsis: 
 notequal( Complex, Complex ); | Complex != Complex;
Description: checks if the arguments are not equal, this is the actual implementation of the FrAid '!=' operator;
Return Value: 
 Boolean
Go to top.


or

Synopsis: 
 or(Boolean, Boolean );       Boolean | Boolean;
Description: logical or, this is the actual implementation of the FrAid '|' operator;
Return Value: 
 Boolean;
Go to top.


quad

Synopsis: 
 quad( Function,Complex, Complex, Complex ); //function, begin, end, number_points
Description:the quadrature of the function from the begin point to the end point (integral)
Return Value: 
 Complex;
Examples: 
quad(sin, -Pi, Pi, 1000);//(-3.3074223103518964E-16 + 0.0i) i.e. 0
Go to top.


rand

Synopsis: 
 rand( );
Description: generate a random number
Return Value: 
 Complex;
Examples: 
rand; // --> (0.2457923314228302 + 0.8490886310240474i)
Go to top.


round

Synopsis: 
 round( Complex );
Description:Rounds (up or down) the real and imaginary parts of its argument.
Return Value: 
 Complex;
Examples: 
round(1.49+1.5i); //--> 1+2i
Go to top.


sign

Synopsis: 
 sign( Complex );
Description:If the argument is positive will return +1, if the argument is negative will return -1, if the argument is 0 will return 0.
Return Value: 
 Complex;
Examples: 
sign(-2); // --> -1
sign(2); // --> 1
sign(0); // --> 0
Go to top.


smaller

Synopsis: 
 smaller( Complex, Complex ); | Complex < Complex;
Description: checks if the first argument is smaller than the second one, if the imaginary part of any of the numbers is not zero takes its absolute value.
This is the actual implementataion of the FrAid '<' operator.
Return Value: 
 Boolean
Go to top.


smallerorequal

Synopsis: 
 smallerorequal( Complex, Complex ); | Complex < Complex;
Description: checks if the first argument is smaller or equal to the second one, if the imaginary part of any of the numbers is not zero takes its absolute value.
This is the actual implementataion of the FrAid '<=' operator.
Return Value: 
 Boolean
Go to top.


sum

Synopsis: 
 sum( Complex [, Complex, Complex, ...] );
Description: sums more than two numbers (add sums only two), sum(a,b,c) is faster than a+b+c (which is add( add( a, b ), c ) )
Return Value: 
 Complex;
Go to top.


xor

Synopsis: 
 xor( Boolean, Boolean ); | Boolean # Boolean;
Description: exclusive or, this is the actual implementataion of the FrAid
Return Value: 
 Boolean
Go to top.


appendS

Synopsis: 
 appendS(SampledFunction1, SampledFunction2);
Description: Appends two vectors (SampledFunctions). Generator Function
Return Value: 
 SampledFunction
Examples: 
f(x)=vector(1,2,3,4);
plot( appendS(f,{-f}) );
Go to top.


cft

Synopsis: 
 cft(ComplexFunction);
Description: Performs a Fourier Transform of a Continious function. The result is a SampledFunction. Generator Function
Return Value: 
SampledFunction
Examples: 
b=1; a=1;
controlVar(a,b);
f(x)=a+b*x;
F(x)=cft(f,20);

plot({abs(F)},{atan(real(F)/imag(F))});
plot(f,icft(F));
Go to top.


cloneS

Synopsis: 
 cloneS(SampledFunction);
Description: Returns a new function identical to the argument but independent from the functions the original depends on (if there are any). Generator Function
Return Value: 
 SampledFunction
Examples: 
a=50;
controlVar( a, 30 );
f(x)=sin(2*Pi*a*x);
fs(x)=sampleL(f, 0, 1, 1000); //fs depends on any change of f(x) and a
fs1(x)=cloneS(fs); //fs1 does not depend on f(x) and a
plot(fs,fs1);
Go to top.


conv

Synopsis: 
 conv( SampledFunction1, SampledFunction2 );
Description:convolution of two vectors
Return Value: 
 SampledFunction
Examples: 
fc(x)=conv(vector(1,2,3,4),vector(4,3,2,1));
printS(fc);
Go to top.


dft

Synopsis: 
 dft( SampledFunction );
Description:Discrete Fourier Transform (not the Fast!)
Return Value: 
SampledFunction (the length of the output is equal of the length of the input)
Examples: 
printS(dft(vector(1,2,3,4)));
Go to top.


dft1

Synopsis: 
 dft1( SampledFunction );
Description:Discrete Fourier Transform (not the Fast!)
Return Value: 
SampledFunction (the length of the output is half + 1 the length of the input)
Examples: 
printS(dft1(vector(1,2,3,4)));
Go to top.


elemS

Synopsis: 
elemS( SampledFunction, Complex1 ); //with two args returns the value of the SampledFunction at index Complex1
elemS( SampledFunction, Complex1, Complex1 ); //with three args changes the value of elem. with number Complex1 to Complex2
Description:Query or change the value of elem. number Complex1.
Return Value: 
The (old) value of elem # Complex1.
Examples: 
f(x)=vector(1,1,1);
a=elemS(f,0); 
a; // --> 1
elemS(f,0,2);
a; // --> 2
f(x)=vector(3,3,3);
a; // --> 3
Go to top.


fft

Synopsis: 
 fft( SampledFunction );
Description:Fast Fourier Transform
Return Value: 
SampledFunction (the length of the output is equal of the length of the input)
Examples: 
printS(fft(vector(1,2,3,4)));
Go to top.


fft1

Synopsis: 
 fft1( SampledFunction );
Description:Discrete Fourier Transform (not the Fast!)
Return Value: 
SampledFunction (the length of the output is half + 1 the length of the input)
Examples: 
printS(fft1(vector(1,2,3,4)));
Go to top.


firResp

Synopsis: 
 firResp( SampledFunction );
Description:Frequency response of a FIR filter (as described in Hamming's book)
Return Value: 
ComplexFunction
Examples: 
f(x)=1;
fs(x)=sampleL(f,0,1,30);    //create a vector
end=2;
controlVar(end);                                    
fst(x)=truncateS(fs,0,end); //get control of the vector's length
fl(x)=fst(x)/lengthS(fst);  //make the sum of the elements allways be 1
plot(fl);
flr(x)=firResp(fl);         //create a function which will follow the freq. response
plot(flr,-.1,1.1,Pi+.1,-.5);
db(x)=8.685890*log(flr(x)); //show in dB
plot(db,-.1,1.1,Pi+.1,-30);
Go to top.


histogramS

Synopsis: 
 histogramS( SampledFunction, Complex1 );
Description:Histogram of the input vector with number of levels passed as second parameter.
Return Value: 
SampledFunction with Complex1 number of elements representing the histogram of the input vector.
Examples: 
sf=10000;
f(x)=recordSound(sf,2048);
plot(f);
plot( histogramS( f, 19 ) );
Go to top.


icft

Synopsis: 
 icft(SampledFunction);
Description: Performs a Inverse Fourier Transform of a Sampled function. The result is a ComplexFunction. Generator Function
Return Value: 
ComplexFunction
Examples: 
b=1; a=1;
controlVar(a,b);
f(x)=a+b*x;
F(x)=cft(f,20);

plot({abs(F)},{atan(real(F)/imag(F))}); //plot the power and phase
plot(f,icft(F));
Go to top.


idft

Synopsis: 
 idft( SampledFunction );
Description:Inverse Discrete Fourier Transform. The length of the output is equal of the length of the input.
Return Value: 
SampledFunction
Examples: 
printS(idft(dft(vector(1,2,3,4))));
Go to top.


idft1

Synopsis: 
 idft1( SampledFunction );
Description:Inverse Discrete Fourier Transform. The length of the output is (len(input)+1)*2.
Return Value: 
SampledFunction
Examples: 
printS(idft1(dft1(vector(1,2,3,4))));
Go to top.


ifft

Synopsis: 
 ifft( SampledFunction );
Description:Inverse Discrete Fourier Transform. The length of the output is equal of the length of the input.
Return Value: 
SampledFunction
Examples: 
printS(ifft(fft(vector(1,2,3,4))));
Go to top.


ifft1

Synopsis: 
 ifft1( SampledFunction );
Description:Inverse Discrete Fourier Transform. The length of the output is (len(input)+1)*2.
Return Value: 
SampledFunction
Examples: 
printS(ifft1(fft1(vector(1,2,3,4))));
Go to top.


inverseFilter

Synopsis: 
 inverseFilter( SampledFunction );
Description:Inverses the filter passed as argument. The frequency response of the resulting filter is flipped vertically.
Return Value: 
SampledFunction
Examples: 
samplingF = 2048;     //Hz
samplingTime = 1;     //seconds
filterLength = 81;    //points
shape(x) = if x < ( samplingF / 2 ) / 3 then 1 else 0; //say limit to a third of the interval
fr(x)=sampleN( shape, 0, 1, samplingF/2+1 ); //freq. response
//plot(fr);

fk(x)=ifft1(fr);                             //filter kernel 1
//plot(fk); 

fkshr(x)=shrotS(fk,filterLength/2);
fktr(x)=truncateS(fkshr,0,filterLength-1);
fkn(x)=fktr(x)/sumS(fktr);                      //normalized kernel

blackmanW(x,filterLength) = 0.42 - 0.5  * cos( 2 * Pi * x / filterLength ) + 0.08 * cos( 4 * Pi * x / filterLength ); //Blackman

wfk(x)=blackmanW(x/stepS(fkn),filterLength)*fkn(x);      //the Blackman windowed filter

fkInv(x)=inverseFilter(wfk);                 //inverse
//fkInv(x)=reverseFilter(wfk);               //reverse

plot(wfk,fkInv);

//check the resulting filters frequency response
efr(x)=firResp(wfk);                      //estimated freq. response 
efrInv(x)=firResp(fkInv);                      //estimated freq. response length 2

plot(efr,efrInv,-.1,1.1,Pi+.1,-.5);
Go to top.


lengthS

Synopsis: 
 lengthS( SampledFunction );
Description:The length of the vector (SampledFunction) passed as argument.
Return Value: 
Complex
Examples: 
lengthS(vector(1,2,3,4)); // --> 4
Go to top.


loadS

Synopsis: 
 loadS( FileName, Start, Step );
Description:Parses a text file with numbers and creates a SampledFunction.
Return Value: 
SampledFunction
Examples: 
f(x)=loadSound("/home/iii/iii123.wav");
plot(f);
playSound(f);
saveS(f,"/home/iii/iii.ttt");
g(x)=loadS("/home/iii/iii.ttt",startS(f),stepS(f));
plot(g);
See also:saveS
Go to top.


maxS

Synopsis: 
 maxS( SampledFunction );
Description:Returns the maximum element of a SampledFunction.
Return Value: 
Complex
Examples: 
maxS(vector(1,2,3,4)); // --> 4
Go to top.


minS

Synopsis: 
 minS( SampledFunction );
Description:Returns the minimum element of a SampledFunction.
Return Value: 
Complex
Examples: 
minS(vector(1,2,3,4)); // --> 4
Go to top.


mulS

Synopsis: 
 mulS( SampledFunction, SampledFunction );
Description:Returns the vector direct product (dyadic) of the input parameters.
Return Value: 
Complex
Examples: 
mulS(vector(1,2,3,4),vector(4,3,2,1)); // --> 20
Go to top.


padS

Synopsis: 
padS( SampledFunction, NewLength );
padS( SampledFunction, NewLength, PadValue);
Description:Returns the input SampledFunction padded to the new length with 0 (the two argument version) or with a new PadValue (the three argument version).
Return Value: 
SampledFunction
Examples: 
printS(padS(vector(1,2,3,4),6,Pi));
printS(padS(vector(1,2,3,4),6));
Go to top.


randS

Synopsis: 
 randS( StartValue, StepValue, Length );
Description:Returns a SampledFunction with the provided StartValue, StepValue, Length and initialized with random Complex values.
Return Value: 
SampledFunction
Examples: 
printS(randS(0,1,5));
Go to top.


reverseFilter

Synopsis: 
 reverseFilter( SampledFunction );
Description:Reverses the filter passed as argument. The frequency response of the resulting filter is flipped horizontally.
Return Value: 
SampledFunction
Examples: 
samplingF = 2048;     //Hz
samplingTime = 1;     //seconds
filterLength = 81;    //points
shape(x) = if x < ( samplingF / 2 ) / 3 then 1 else 0; //say limit to a third of the interval
fr(x)=sampleN( shape, 0, 1, samplingF/2+1 ); //freq. response
//plot(fr);

fk(x)=ifft1(fr);                             //filter kernel 1
//plot(fk); 

fkshr(x)=shrotS(fk,filterLength/2);
fktr(x)=truncateS(fkshr,0,filterLength-1);
fkn(x)=fktr(x)/sumS(fktr);                      //normalized kernel

blackmanW(x,filterLength) = 0.42 - 0.5  * cos( 2 * Pi * x / filterLength ) + 0.08 * cos( 4 * Pi * x / filterLength ); //Blackman

wfk(x)=blackmanW(x/stepS(fkn),filterLength)*fkn(x);      //the Blackman windowed filter

//fkInv(x)=inverseFilter(wfk);                 //inverse
fkInv(x)=reverseFilter(wfk);               //reverse

plot(wfk,fkInv);

//check the resulting filters frequency response
efr(x)=firResp(wfk);                      //estimated freq. response 
efrInv(x)=firResp(fkInv);                      //estimated freq. response length 2

plot(efr,efrInv,-.1,1.1,Pi+.1,-.5);
Go to top.


rk

Synopsis: 
rk( Function1, ..., FunctionN, //the system
    Complex1, ..., ComplexN,   //the initial conditions
    Complex, Complex, Complex, //the time constraints - start point, end point, number fo samples
    String );                  //prefix of the function names to be registered/returned (see the example bellow)
Description: registers N one argument functions named _rk_0(x), _rk_1(x), ... _rk_{N-1}(x) in the symbol table;
they are not treated as UserDefinedFunctions if the number of samples is too big (for a high resolution plot it may take 10,000 and more), the printDef() function may not function properly;
Return Value: 
 - how many functions were successfully registered in the symbol table, should be N
Examples: 
sigma = 10;
b = 8/3;
r = 28;
t0 = 0;
tn = 100;
steps = 10000;
lor1( x1, x2, x3, t ) = sigma * (x2 - x1);
lor2( x1, x2, x3, t ) = r*x1 - x2 - x1*x3;
lor3( x1, x2, x3, t ) = x1*x2 - b*x3;
rk(    lor1,//the system
       lor2,
       lor3,
       0, 1, 0,                //the initial condition
       t0,                     //the start point
       tn,                     //the end point
       steps,                  //number of samples
       "_rk"                   //prefix of the return function names
                               //in this case _rk_0, _rk_1 and _rk_2
                               //will be registered
);
plot2(_rk_0,_rk_2,t0,tn);
Go to top.


rk1

Synopsis: 
rk1( Function1, ..., FunctionN, //the system
    FunctionN+1, ..., Function2N,   //the initial conditions
    Function2N+1, Function2N+2, Function2N+3, //the time constraints - start point, end point, number fo samples
    String );                  //prefix of the function names to be registered/returned (see the example bellow)
Description: This is a variation of rk() which takes function references for arguments and listens for changes
Return Value: 
 - how many functions were successfully registered in the symbol table, should be N
Examples: 







See also: rk





Go to top.











sampleL








Synopsis:

 sampleL( ComplexFunction, StartPoint, EndPoint, NumberOfSamples );







Description:Samples the given Complex.





Return Value:

SampledFunction







Examples:

a=50;
controlVar( a, 30 );
f(x)=0.7*sin(2*Pi*a*x) + sin(2*Pi*120*x); //compose a signal
fs(x)=sampleL(f, 0, 1, 1000);
F(x)=dft1(fs);
plot({abs(F)},{atan( real(F) / imag(F))});
plot(fs,idft1(F));







Go to top.











sampleN








Synopsis:

 sampleN( ComplexFunction, StartPoint, Step, NumberOfSamples );







Description:Samples the given Complex.





Return Value:

SampledFunction







Examples:

a=50;
controlVar( a, 30 );
f(x)=0.7*sin(2*Pi*a*x) + sin(2*Pi*120*x);
fs(x)=sampleL(f, 0, 1, 1000);
fr(x)=sampleN(f, 0, 1/1000, 1000);
plot(fs,fr);







Go to top.











samples








Synopsis:

 samples( StartValue, Step, Value1, Value2, ... );







Description:Creates a SampledFunction with StartValue, Step and values supplied as parameters Value1, Value2, etc...





Return Value:

SampledFunction







Examples:

f(x)=samples(2,2,0,1,0,1,0,1,0);
plot(sampleL(f,startS(f),startS(f)+stepS(f)*lengthS(f), 100));







See also:vector





Go to top.











saveS








Synopsis:

 saveS( SampledFunction, FileName );







Description:Converts a SampledFunction to a character string of comma separated numbers and saves it to FileName.





Return Value:

0







Examples:

f(x)=saveSound("/home/iii/iii123.wav");
plot(f);
playSound(f);
saveS(f,"/home/iii/iii.ttt");
g(x)=loadS("/home/iii/iii.ttt",startS(f),stepS(f));
plot(g);







See also:loadS





Go to top.











shrotS








Synopsis:

 shrotS( SampledFunction, numberToShiftRotate );







Description:Shift-rotate the given SampledFunction by numberToShiftRotate





Return Value:

SampledFunction







Examples:

printS(shrotS(vector(1,2,3,4), 2)); // --> 3,4,1,2







Go to top.











startS








Synopsis:

startS( SampledFunction );
startS( SampledFunction, newStartValue );







Description:Returns the start value of the given SampledFunction. If called with three args changes the start value.





Return Value:

Complex







Examples:

startS(samples(6,5,4,3,2,1)); // --> 6 







Go to top.











stepS








Synopsis:

stepS( SampledFunction );
stepS( SampledFunction, newStepValue );







Description:Returns the step value of the given SampledFunction. If called with three args changes the step value.





Return Value:

Complex







Examples:

stepS(samples(6,5,4,3,2,1)); // --> 5 







Go to top.











sumS








Synopsis:

 sumS( SampledFunction );







Description:Sums the elements of the given SampledFunction.





Return Value:

Complex







Examples:

sumS(vector(1,2,3,4)); // --> 10







Go to top.











truncateS








Synopsis:

 truncateS( SampledFunction, startIndex, endIndex );







Description:Truncate the passed SampledFunction from startIndex (0 based) to endIndex inclusive.





Return Value:

SampledFunction







Examples:

printS(truncateS(vector(1,2,3,4),0,2)); // --> 1,2,3







Go to top.











vector








Synopsis:

vector( Value1, Value2, ... );







Description:Creates a SampledFunction with StartValue=0, Step=1 and values supplied as parameters Value1, Value2, etc...





Return Value:

SampledFunction







Examples:

f(x)=vector(0,1,0,1,0,1,0);
plot(sampleL(f,startS(f),startS(f)+stepS(f)*lengthS(f), 100));







See also:samples





Go to top.











loadSound








Synopsis:

 loadSound( fileName );







Description:Loads an audio file (of type supported by your JRM) to a SampledFunction





Return Value:

SampledFunction







Examples:

plot(loadSound("/home/iii/iii123.wav"));







Go to top.











playSound








Synopsis:

 playSound( SampledFunction );







Description:Play a SampledFunction through the sound card. Opens a play controller.





Return Value:

0







Examples:

playSound( loadSound("/home/iii/iii123.wav") );







Go to top.











recordSound








Synopsis:

recordSound( SamplingFrequency, bufferSize );







Description:Opens a record sound controller and starts listening for input from the sound card.





Return Value:

SampledFunction







Examples:

sf=10000;
f(x)=recordSound(sf);
plot(f,0,.01,1,-.01);
plot({abs(fft1(f))});







Go to top.











saveAsSound








Synopsis:

saveAsSound( SampledFunction, fileName );







Description:Save the given SampledFunction to an audio file.





Return Value:

0







Examples:

f(x)=loadSound("/home/iii/iii123.wav");
saveAsSound( f, "/home/iii/iii123_test.wav" );







Go to top.











aggregation








Synopsis:

aggregation( [Complex*,] /*optional window number*/);







Description:





Return Value:

 Complex - the window number







Plugin Features





Left Mouse Button:if plot is not active will start a new diagram with origin in the click point, if plot is active will stop it;





Middle Mouse Button:     zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button:        popup menu





Popup Menu Commands:





Keyboard shortcuts:














Examples:

aggregation();







Go to top.











cobweb








Synopsis:

cobweb( [Complex*,]                //optional window number
        [Function*,...]              //list of functions
        [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
        [Complex, Complex]); //optional window size (width, height)







Description: plots a cobweb diagram





Return Value:

 Complex - the window number







Plugin Features





Left Mouse Button:          click and a new diagram will be plotted with starting point where you clicked;





Middle Mouse Button:     zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button:        popup menu





Popup Menu Commands:





Autoscale: will try to fit the plot into the window





Colors:





Keyboard shortcuts:














Examples:

f(x)=3.75*x*(1-x);
cobweb(f);







Images: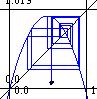image





See also:_plot





Go to top.











color3D








Synopsis:

color3D( [Complex*,] /*optional window number*/
         Function* ); //the function to plot







Description: plots a diagram with the assigned colors of the 2 argument function passed





Return Value:

 Complex - the window number







Plugin Features





Left Mouse Button:         





Middle Mouse Button:     zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button:        popup menu





Popup Menu Commands:





Keyboard shortcuts:














Examples:

        f(x,y) = x*y;
        color3D(f);







Go to top.











consumption








Synopsis:








Description:Experimental function...





Return Value:








Go to top.











iterFract








Synopsis:

iterFract( [Complex*,]                //optional window number
           Function*, Complex*, //first     function and xOffset of the first transform
           Function*, Complex*, //second function and yOffset of the first transform
           [Function*, Complex*, //first     function and xOffset of the next transform
           Function*, Complex*, //second function and yOffset of the next transform
           ...]);







Description: [iterativeFractals] iterates a set of contracting transformations iter fract





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button:draw the image to transform, every click fixes a point (corner), press Shift for the last point;





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:Step - will plot the next transformed image, if the replaceLast setting is true the previous image will be deleted





Autoscale: won't do anything





Colors: you can set every subsequent step to use a different color; background color;





Keyboard shortcuts:

 press the Shift key to mark the final point of your initial image;













Examples:

        To plot the image on the top start with:

            ff(r,a,off,x,y)=r*cos(a)*x - r*sin(a)*y + off; //the generic transformation
            gg(r,a,off,x,y)=r*sin(a)*x + r*cos(a)*y + off;

            r1=.5; //the parameters I want to control for the first transform
            a1=Pi/4;
            xOff1=0;
            yOff1=0;
            controlVar(r1, a1,xOff1, yOff1 ); //variable controller

            f1(x,y)=ff(r1,a1,0,x,y); //the first transform
            g1(x,y)=gg(r1,a1,0,x,y);

            r2=.5; //the parameters I want to control for the first transform
            a2=-Pi/3;
            xOff2=0;
            yOff2=0;
            controlVar(r2,a2,xOff2,yOff2); //variable controller

            f2(x,y)=ff(r2,a2,0,x,y); //the second transform
            g2(x,y)=gg(r2,a2,0,x,y);

            iterFract(  f1,xOff1, //first
                        g1,yOff1,
                        f2,xOff2,  //second
                        g2,yOff2 );

         draw the blue  figure,

             iter initial

        click Step from the popup and with the sliders adjust the two green transformed  images
        now if you start iterating (using Step or Iterate from the popup ) you'll get the attractor of the system;

        A three transforms plot and starting with a single line can give you:

            little tree  or little tree 2

            or  starting with a triangle and changing the replaceLast setting to false
            (note what happens when you change the parameters; use the sliders)
            







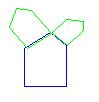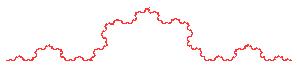Images:image,

        
image, - begin with this;

        
image,
        image,

        
image,
        image,
        image,

        
image		





See also: transform 





Go to top.











julia








Synopsis:

julia( [Complex*,]           //optional window number
       [Function*,...]       //list of functions
       [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
       [Complex, Complex]); //optional window size (width, height)







Description: given a complex function plots a julia fractal   julia1 in any number of colors  julia
 it is generally quite slow, start with a small window, adjust the colors and iteration numbers and when you get the desired look, go large;





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button: play the fractals iterations at this point (opens a MIDI panel);





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale: will not work for this type of plot





Colors:
            * if you specify exatly two colors, the number of iterations will be determined by the iterationLimit setting (choose Settings from the popup menu);                                                        two color julia  (a two color fractal )

            * if the colors are more than two, their number will determine how many iterations will be performred for each point on the panel (Hint: the more colors (iterations) you choose the more well defined your fractal will be; depeding on the function you use, a value of 500-600 would render a very good printable 3500x4000 pix image );		





Keyboard shortcuts:














Examples:

        c=-0.122+0.745i;
        f(z)=z^2+c;
        julia(f);







Images:image,image,image





See also: _plot 





Go to top.











mandelbrot








Synopsis:








Description: plots the specified functions (undocumented)





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: drag to rotate the image





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

clear();
a=2;
controlVar(a);
f(z,c)=z^a+c;
mandelbrot( f );







See also: julia





Go to top.











newton








Synopsis:








Description:Experimental function... When finished should plot the fractal associated with Newton's method





Return Value:








Go to top.











orbit








Synopsis:

orbit( [Complex*,]          //optional window number
       [Function*,...]      //list of functions
       [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
       [Complex, Complex]); //optional window size (width, height)







Description:  plots a orbit diagram                 orbit,

takes a two argument function, the first is a variable (oordinate), the second is a parameter (abscissa)		





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button: zoom after middle button selection





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale: will try adjust the number of plot and settle iterations for maximum image definition (see the numberIterations and settleNumber settings)





Colors: you can choose background and plot colors; 





Keyboard shortcuts:














Examples:

        f(x,r)=r*x*(1-x);
        orbit(f);

        will generate the image on the first line of this section.

        Or the following script will generate the image on the right:       orbit2

        f(x,p)= if x < 0 then 0 else
                if (x >= 0) & (x < 1/2) then p*x else
                if (x >= 1/2) & (x < 1) then -p*x+p else 0;
        orbit(f);







Images:image,image





See also: _plot 





Go to top.











orbit2








Synopsis:

orbit2( [Complex*,]          //optional window number
       XFunction, YFunction      //list of functions
       [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
       [Complex, Complex]); //optional window size (width, height)







Description:plots a orbit2 diagram





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button: zoom after middle button selection





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: you can choose background and plot colors; 





Keyboard shortcuts:














Examples:

fx( x, y ) = 1 - y + abs( x );
fy( x, y ) = x;
orbit2( fx, fy );







Go to top.











phase








Synopsis:

phase(  [Complex*,]                //optional window number
	[Function*,...]            //list of functions
	[Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
	[Complex, Complex]);       //optional window size (width, height)







Description: plots the vector field and phase diagram for a given second order differential equation phase
 even if your equation is homogenious you need to have an independent variable in the argument list





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button: will plot the trajectory starting at this point





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands: StartPoints submenu, controls the number of the start points





Autoscale: will try to fit the plot into the window





Colors: plotColor, directionFieldColor, backgroundColor





Important settings: (all are positive)

            deltaDenominator - determines how smooth your trajectories will be (the larger this number more smooth and slower plot);

            timeLength - determines how long your trajectories will be;

            distanceBetweenVectors - (in pixels) determines how close your vectors will be on the plot;

            vectorDenominator - determines the size of the vectors (the larger this number the shorter the vectors);		





Keyboard shortcuts:














Examples:

        f(x,y,t)= x - y;
        g(x,y,t)= 1 - x^2;
        phase( f, g );







Images:image





Go to top.











plot








Synopsis:

plot( [Complex*,]          //optional window number
      [Function*,...]      //list of functions
      [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
      [Complex, Complex]); //optional window size (width, height)







Description:plots the specified functions plot





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: add a grid mark





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale: will try to fit the plot into the window





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

        f(x)=sin(2*x)+sin(3*x);
        plot(g),log);







Images: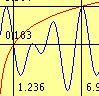image





Go to top.











plot2








Synopsis:

plot2( [Complex*,]                     //optional window number
       Function*,Function* ,           //the two functions
       Complex, Complex,               //the start and end points of the independant variable
       [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
       [Complex, Complex]);           //optional window size (width, height)







Description: plots two functions relative to each other plot2





Return Value:

 Complex - the window number;







Plugin Features





Left Mouse Button: zoom after middle button selection





Middle Mouse Button: zoom in (move the mouse left to right, up to down),
 zoom out (move the mouse from right to left and down up);		





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale: will try to fit the plot into the window





Colors: background, plot 





Keyboard shortcuts:














Examples:

        f(x)=sin(2*x)+sin(3*x);
        plot2( sin, f,0 ,2*Pi );







Images: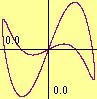image





Go to top.











plot3








Synopsis:








Description: plots the specified functions (undocumented)





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: drag to rotate the image





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

 - see the demo on fraid.org







Go to top.











plot3d








Synopsis:








Description: plots the specified functions (undocumented)





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: drag to rotate the image





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

 - see the demo on fraid.org







Go to top.











plot3f








Synopsis:








Description: plots the specified functions (undocumented)





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: drag to rotate the image





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

 see the demo on fraid.org







Go to top.











plotMap








Synopsis:

plotMap([Complex*,]                //optional window number
	[Function*,...]              //list of functions
	[Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
	[Complex, Complex]); //optional window size (width, height)







Description:plots the development in time of an iterative map plotmap





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: will plot a new map starting from the selected point (determines the value of the map parameter );





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale: will try to fit the plot into the window





Colors: 





Keyboard shortcuts:














Examples:

	g(x)=3.95*x*(1-x);
	plotMap(g);







Images:image





Go to top.











spectrum








Synopsis:

 spectrum( SampledFunction, length );







Description:Discrete Fourier Transform (not the Fast!)





Return Value:

Plots the spectrum of a SampledFunction. The abscissa is time, the ordinate is frequency. The amplitude for each frequency at any moment of time is color coded according to the plot settings (right click->Settings->plotColors).







Examples:

sf=10000;
f(x)=recordSound(sf);
plot(f,0,.01,1,-.01);
a=spectrum(f,512);
plotOption(a,"threshold",.1);







Go to top.











transform








Synopsis:

transform([Complex*,]          //optional window number
          Function*, Function* //the transform, linear or not
          [Complex, Complex, Complex, Complex]  //optional upper left and bottom right 2D plane corner coordinates
          [Complex, Complex]); //optional window size (width, height)







Description:  will transfrom a mouse entered 2D image transform; Takes two, two argument functions.

You can animate your transformations by setting the iterate and delay_ms settings:

animate		





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: draw the image to transform, every click fixes a point (corner), press Shift for the last point;





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands: Step - will plot the next transformed image, if the replaceLast setting is true the previous image will be deleted





Autoscale: won't do anything





Colors: background, plot 





Keyboard shortcuts:

 press the Shift key to mark the final point of your initial image;













Examples:

ff(r,s,a,b,off,x,y)=r*cos(a)*x - s*sin(b)*y + off; //first transform equation
gg(r,s,a,b,off,x,y)=r*sin(a)*x - s*cos(b)*y + off; //second transform equation
r1=1;                                              //x scaling
s1=1;                                              //y scaling
a1=Pi/4;                                           //first angle
b1=3*Pi/4;                                         //second angle
xOff1=0.05;                                        //x offset
yOff1=0;                                           //y offset
controlVar(a1, b1,xOff1, yOff1, r1, s1 );    //GUI control for the variables
f1(x,y)=ff(r1,s1,a1,b1,xOff1,x,y);
g1(x,y)=gg(r1,s1,a1,b1,yOff1,x,y);
transform(f1,g1);








Images: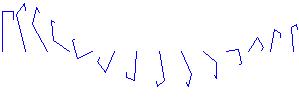image,image





See also: iterFract 





Go to top.











transform3








Synopsis:








Description: plots the specified functions (undocumented)





Return Value:

 Complex - the window number where the functions were plot;







Plugin Features





Left Mouse Button: drag to rotate the image





Middle Mouse Button: zoom in (move the mouse left to right, up to down), zoom out (move the mouse from right to left and down up);





Right Mouse Button: popup menu





Popup Menu Commands:





Autoscale:





Colors: a multycolor color map, each function can have its own color, background color; 





Keyboard shortcuts:














Examples:

see the demo on fraid.org







Go to top.











pmChart








Synopsis:








Description:Experimental function...





Return Value:








Go to top.











predictionMarket








Synopsis:








Description:Experimental function...





Return Value:








Go to top.











abs








Synopsis:

  abs( Complex );







Description:returns the absolute value of it's argument;





Return Value:

 Complex, imaginary part = 0;







Examples:

         abs(3+6i);  // (6.708203932499369 + 0.0i)
         abs(-2);      // (2.0 + 0.0i)







Go to top.











acos








Synopsis:

 acos(Complex);







Description: arccos





Return Value:

 Complex







Examples:








Go to top.











acosh








Synopsis:

 acosh( Complex );







Description: hyperbolic arccos





Return Value:

 Complex







Examples:








Go to top.











add








Synopsis:

 add(Complex , Complex );







Description:this is the actual implenetation of the FrAid '+' operator.





Return Value:

Complex







Examples:

      add(3+4i,5+6i);          // (8.0 + 10.0i), same as 3+4i + 5+6i








Go to top.











asin








Synopsis:

 asin( Complex );







Description: arcsine





Return Value:

 Complex







Go to top.











asinh








Synopsis:

 asinh( Complex );







Description: hyperbolic arcsine





Return Value:

 Complex







Go to top.











atan








Synopsis:

 atan(Complex)







Description: arctangens





Return Value:

 Complex







Go to top.











atanh








Synopsis:

 atanh( Complex );







Description: hyperbolic arctangens





Return Value:

 Complex







Go to top.











conj








Synopsis:

 conj( Complex );







Description: returns the complex conjugate of its argument;





Return Value:

 Complex







Examples:

  conj(3+4i); //(3.0 - 4.0i)
  conj(3-4i);  //(3.0 + 4.0i)







Go to top.











cos








Synopsis:

 cos( Complex );







Description:cosine





Return Value:

 Complex







Go to top.











cosec








Synopsis:

 cosec( Complex );







Description: cosecant





Return Value:

 Complex







Go to top.











cosh








Synopsis:

 cosh( Complex );







Description: hyperbolic cosine





Return Value:

 Complex







Go to top.











cot








Synopsis:

 cot( Complex );







Description:cotangent





Return Value:

 Complex







Go to top.











divide








Synopsis:

 divide( Complex, Complex ); | Complex / Complex;







Description: division function, this is the actual implementation of the FrAid '/' operator;





Return Value:

 Complex







Go to top.











equal








Synopsis:

 equal( Complex | String, Complex | String ); | Complex | String == Complex | String;







Description: checks if its arguments for equality, works for both Complex and String, this is the actual implementation of the FrAid '==' operator;





Return Value:

 1 if equal else 0







Examples:

  "Hi"=="Hi"; //1
  "Hi"=="Hi."; //0
  equal( "Hi", "Hi" ); //1
  equal( "Hi", "Hi." ); //0
  equal( "Hi", 7 ); //0







Go to top.











exp








Synopsis:

 exp( Complex );







Return Value:

 Complex







Go to top.











imag








Synopsis:

 imag( Complex )







Description: the imaginary part of its argument





Return Value:

 Complex, with imaginary part 0;







Go to top.











log








Synopsis:

 log( Complex );







Description: logarithm





Return Value:

 Complex







Go to top.











multiply








Synopsis:

 multiply( Complex, Complex ); | Complex * Complex;







Description: multilies its arguments, this is the actual implementation of the FrAid '*' operator;





Return Value:

 Complex







Go to top.











power








Synopsis:

 power( Complex, Complex ); | Complex^Complex;







Description: the first argument power the second one, this is the actual implementation of the FrAid '^' operator;





Return Value:

 Complex







Go to top.











real








Synopsis:

 real( Complex );







Description:the real part of a Complex number





Return Value:

 Complex, the imaginary part will be zero;







Go to top.











sec








Synopsis:

sec( Complex );







Description: secant;





Return Value:

 Complex;







Go to top.











sin








Synopsis:

 sin( Complex );







Description: sine function;





Return Value:

 Complex







Go to top.











sinh








Synopsis:

 sinh( Complex );







Description:hyperbolic sine;





Return Value:

 Complex







Go to top.











sqrt








Synopsis:

 sqrt( Complex );







Description: square root





Return Value:

 Complex;







Go to top.











subtract








Synopsis:

 subtract( Complex, Complex); | Complex - Complex;







Description: subtracts the second argument from the first one, this is the actual implementataion of the FrAid '-' operator;





Return Value:

 Complex







Go to top.











tan








Synopsis:

 tan( Complex );







Description: tangent;





Return Value:

 Complex







Go to top.











tanh








Synopsis:

 tanh( Complex );







Description: hyperbolic tangent;





Return Value:

 Complex







Go to top.











assign








Synopsis:

 assign( UserDefinedVariable*, Complex* );







Description: Assigns a complex value to the specified no argument function.
 Use in FrAid defined functions (see example).
 As a side effect lets you animate your graphics.		





Return Value:

 the value assigned - Complex







Examples:

A very basic example:
      a=5;
      assign(a, 3); //same as just a = 3;
      a;
      assign(a, sin(Pi/3));
      a;

A more meaningful example:
      a=1;
      iterate( startValue, endValue, step ) =
      if startValue > endValue
      then 0
      else assign( a, startValue ) &
           iterate( startValue + step, endValue, step );
      f(x)=sin(a*x);
      plot(f);
      iterate( 1, 20, .2);







Go to top.











loadSymbols








Synopsis:

 loadSymbols( Boolean, String* );







Description: controls the packages loaded in the symbol table;

if the first argument is not 0 loads the specified package in the symbol table, else unloads;

the second argument could be a directory relative from the system property FRAIDPATH or name of a class implementing the StaticSymbolsInterface (used in applets).		





Return Value:

 the number of the successfully loaded/unloaded functions - Complex;







Examples:

loadSymbols(1,"org.fraid.symbtable.StaticSymbols");   //load from a class
loadSymbols(True,"bin/org/fraid/graphics/functions"); //load from a directory, note the missing slashes
//at the begining and end of the string







Go to top.











False








Synopsis:

 False;







Description: more readable version of (0+0i) where a Boolean value is expected;





Return Value:

 0+0i;







Go to top.











True








Synopsis:

 True;







Description: a shorthand for 1 where a Boolean is expected;





Return Value:

 (1+0i)







Go to top.











debug








Synopsis:

 debug([Boolean]);







Description: toggles the debug option;
  if called without arguments returns the current debug state, if called with argument returns the value before the change;		





Return Value:

 Boolean 







Go to top.











debugParser








Synopsis:

debugParser();
debugParser(Boolean);







Description:Turns debugging of the parser on or off. Without arguments just prints the current value (0=false,1=true). To prevent excessive outpute turn on for the line(s) of FrAid code you are interested in.





Return Value:

0 (false) or 1 (true) - depending on what the last setting was.







Examples:

debugParser(True);
plot({sin+cos});
debugParser(False);







Go to top.











exit








Synopsis:

 exit( [Complex] );







Description: the real part of the argument is treated as an exit value;  closes the current application;





Return Value:

 Complex;







Go to top.











info








Synopsis:

 info;







Description: version and license info;





Return Value:

 String;







Go to top.











isComplex








Synopsis:

 isComplex( Complex );







Description: checks if the specifeied argument does not evaluate to a String;





Return Value:

 Boolean







See also: Types 





Go to top.











isFunction








Synopsis:

 isFunction( Complex );







Description: checks if the specifid argument is a Function;





Return Value:

 Boolean







See also:  Types 





Go to top.











isString








Synopsis:

 isString( Complex );







Description: checks if the specified argument is a String;





Return Value:

 Boolean







Examples:

isString(printDef()); // 1







See also:  Types 





Go to top.











loadScript








Synopsis:

loadScript( fileName );







Description:Loads a FrAid script from the given file. Returns the value of the last executed command in the script.





Return Value:

Complex







Examples:

loadScript("/home/aaa/myFrAidScript.frd");







Go to top.











printClassPath








Synopsis:

 printClassPath();







Description: Prints the class path after FrAid manipulated it. Use for troubleshooting.





Return Value:

 String







Go to top.











printDef








Synopsis:

 printDef( [Function [, Function,...]] );







Description: does not return dependancies like printDep but only the definition of the function;
  returns a string with the definition of a function or with no arguments all functions in the symbol table; this is the former dump function.		





Return Value:

 String







Examples:

g(x)=x+1;
h(x)=x*x*x;
f(x,y)=h(x)^g(y)-1;
printDef(f); // f( x, y ) = subtract( power( h( x ), g( y ) ), 1.0 );
printDef(sin); /*Java defined function:sin( _0 );*/







Go to top.











printDep








Synopsis:

 printDep( [UserDefinedFunction*] );







Description: returns a string with the specified functions dependancies or all dependancies;

if a function f(...) calls (depends on) g(...) and h(...) the complete definition of f(...) should include g(...) and h(...); use this function to save your sessions; this is the former dumpAll function.		





Return Value:

 String







Examples:

      g(x)=x+1;
      h(x)=x*x*x;
      f(x,y)=h(x)^g(y)-1;
      printDep(f);

Result:
      /*Java defined function:subtract( _0, _1 );*/
      /*Java defined function:power( _0, _1 );*/
      /*Java defined function:add( _0, _1 );*/
      g( x ) = add( x, 1.0 );
      /*Java defined function:multiply( _0, _1 );*/
      h( x ) = multiply( multiply( x, x ), x );
      f( x, y ) = subtract( power( h( x ), g( y ) ), 1.0 );







Go to top.











printGen








Synopsis:

 printGen( [Function [, Function,...]] );







Description:For GeneratedFunction(s) returns a string with the definition of the function(s). For non-generated functions returns an empty string.





Return Value:

String







Examples:

printGen(vector(1,2,3,4));







Go to top.











printPlugins








Synopsis:

 printPlugins();







Description: Prints the plugins visible for FrAid. Use for troubleshooting or to see if you need a certain plugin.





Return Value:

 String







Go to top.











printS








Synopsis:

printS( SampledFunction );







Description:Prints the definition of a sampled function. May be unstable when called on very long SampledFunctions.





Return Value:

String







Examples:

printS(vector(1,2,3,4));







Go to top.











printTree








Synopsis:

 printTree( UserDefinedFunction* );







Description: prints the parse tree of the specified user defined function; this is the former dumpTree function





Return Value:

 String







Examples:

      g(x)=x+1;
      h(x)=x*x*x;
      f(x,y)=h(x)^g(y)-1;
      printTree(f);

Result:
FunctionCall = subtract( power( h( x0 ), g( x1 ) ), 1.0 ) :ExecutableFunction
 FunctionCall = power( h( x0 ), g( x1 ) ) :ExecutableFunction
  FunctionCall = h( x0 ) :ExecutableFunction
   Variable = x0 :null
  FunctionCall = g( x1 ) :ExecutableFunction
   Variable = x1 :null
 ImaginaryNumber = 1.0 :null







Go to top.











rename








Synopsis:

 rename( ComplexFunction, newName );







Description:Renames the given FrAid variable or function to the new name. Returns the old name.





Return Value:

String







Examples:

a=1;
a;
rename(a,"bb");
a; // Error
bb; // --> 1







Go to top.











sleep








Synopsis:

 sleep( Complex );







Description: sleeps the specified interval in milliseconds





Return Value:

 0







Go to top.











string








Synopsis:

 string( Arg1, Arg2, ... );







Description:Returns a string which is the concatenation of the string values of the given arguments.





Return Value:

String







Examples:

myString=string(1," is smaller than ",3);







Go to top.











typeOf








Synopsis:

 typeOf( Complex );







Description: returns a string representing the Type of the given argument;





Return Value:

 String, three possible values "Complex", "String" and "ComplexFunction" (the UserDefinedFunctions are ComplexFunctions)







Examples:

h(x)=x*x*x;
typeOf(h); //ComplexFunction
typeOf(sin);//ComplexFunction
typeOf(printDef);//String
typeOf("hello");//String
typeOf(2);//Complex







Go to top.











clear








Synopsis:

 clear([ UserDefinedFunction*, UserDefinedFunction*, ... ]);







Description:called with no arguments removes all user defined functions from the symbol table;called with a list of arguments removes all functions in the list from the symbol table;





Return Value:

 the number of the functions removed - Complex







Examples:

a=5; b=6; f(x,y)=x^y;
printDep;
clear(a);
printDep;
clear();
printDep;







Go to top.











closeControllers








Synopsis:

closeControllers();







Description:Closes all open variable controllers.





Return Value:

Complex







Examples:

a=1; b=2; c=3;
controlVar(a,b);
controlVar(c);
closeControllers; //closes all of them








Go to top.











closeWindow








Synopsis:

 closeWindow( Complex [, Complex, ... ] );







Description: prints the numbers of variable listeners disconected;  closes the specified graphics windows;





Return Value:

 the number of successfully closed windows







Examples:

myWindow = plot( sin );
closeWindow( myWindow );







Go to top.











controlVar








Synopsis:

 controlVar( UserDefinedVariable* [, UserDefinedVariable*, UserDefinedVariable*, ... ] );







Description: opens a control window which contains a list of sliders allowing interactive change of the specified variables;
pass a list of variables to control interactively. Convenient whith graphics of functions and especially transforms dependant on external variables.





Return Value:

 the number of the successfully added to the control window variables - Complex;







Examples:

a=1; b=1;
controlVar(a,b);
f(x)=(a*sin(b*x));
plot(f);







Go to top.











plotOption








Synopsis:

plotOption(windowNumber);
plotOption(windowNumber,optionName);
plotOption(windowNumber,optionName, newValue);







Description:With no arguments returns a list of all the options(settings) and their types defined for the given window (specified by its window number). 
With one argument returns the value of the option/setting with the given name. If the option is composite prints the names and types of its members.
With two arguments sets the option with the given name to the newValue and returns the old one.
For boolean options pass 0 or 1.
For string options pass a String.
For all numeric options (int, double, etc.) pass a Complex.






Return Value:

Number or String depending on what the option is.







Examples:

sf=10000;
f(x)=recordSound(sf);
plot(f,0,.01,1,-.01);
a=spectrum(f,512);
plotOption(a,"threshold",.1);







Go to top.











printWindowFunction








Synopsis:

 printWindowFunction( Complex [, Complex, ... ] );







Description: returns a string with the definition of the function(s) being ploted to the specified graphics window;





Return Value:

 String







Examples:

h(x)=x*x*x;
myWindow = plot(h);
printWindowFunction(myWindow); //result -> h( x ) = multiply( multiply( x, x ), x );







Go to top.











setGridMark








Synopsis:

setGridMark( windowNumber, X, Y );







Description:Sets a new grid mark to the given window at location X:Y.





Return Value:

0







Examples:

setGridMark(plot(sin),0,0); //open a new plot with the origin marked







Go to top.